Källa: http://magnus-karlsson.nu/mandel/matematik.php

Matematik

Mandelbrotmängden

Matematiken bakom

Hur bilderna av mandelbrotmängden har uppstått tänkte jag berätta i det följande. För att du ska hänga med krävs att du vet något om imaginära och komplexa tal.
Har du ingen aning om vad som menas med detta bör du först läsa sidan om komplexa tal.

Först lite teori

Tänk dig att vi väljer ut ett tal i det komplexa talplanet och kallar det för c. Vi tilldelar sedan talet z₀ värdet 0 + 0i, dvs origo. Beräkna nu värdet av z₁ på följande sätt:

z₁ = z₀² + c

Beräkna nu ett värde på z₂ genom att upprepa proceduren ovan. Om vi håller på så här ett tag kommer vi att få en lång följd av tal z₁, z₂, z₃ och så vidare upp till z_n.

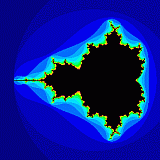
Om vi beräknar avståndet till origo för vart och ett av dessa tal kommer vi att få en följd av reella tal. Om vi finner att denna reella talföljd närmar sig värdet 0 när n blir stort så säger vi att talet c, som vi började med, tillhör mandelbrotmängden. Alla de komplexa tal som är markerade med svart i bilden tillhör mandelbrotmängden. Om talföljden inte närmar sig noll tillhör c inte mandelbrotmängden.

Man kan bevisa att om avståndet mellan origo och ett komplext tal är större än två kommer avståndet till origo för alla efterföljande tal i serien alltid att öka, dvs talet tillhör inte mandelbrotmängden.

"Var kommer alla färgerna ifrån då?" undrar du. Jo, beroende på hur länge man behöver räkna för att avgöra om ett visst c kommer att passera gränsen och gå mot oändligheten eller inte kan man ge den punkt som motsvarar c i talplanet en viss färg. I mina bilder blir punkten blå om det krävs få beräkningar och sedan får punkten allt rödare färg ju fler beräkningar som behövs.

Ett annat (roligare) sätt att förklara kan du läsa här:
http://fy.chalmers.se/~tomten/Dikter/Albrecht.html

Några exempel

Verkar det här krångligt? Då kommer här några exempel för att belysa teorin.

Exempel 1

Vi börjar med att välja ut ett c till exempel c = 0,5 + 0,5i.
Beräkna z₁ = z₀² + c = (0 + 0i)² + 0,5 + 0,5i = 0,5 + 0,5i.
Nästa steg är att beräkna avståndet från origo till detta tal, det gör vi med pytagoras sats.
Avståndet = (0,5² + 0,5²) = 0,707...

Vi räknar nu ut nästa z på följande sätt:
z₂ = z₁² + c = (0,5 + 0,5i)² + 0,5 + 0,5i = 0,5 + 1,0i.
Avståndet till origo blir 1,25 = 1,118...

Och så är det bara att fortsätta...

Om vi för in våra resultat i en tabell ser det ut så här:

n	z_n	Avstånd till origo
1	0,5 + 0,5i	0,707...
2	0,5 + 1,0i	1,118...
3	-0,25 + 1,5i	1,520...
4	-1,6875 - 0,25i	1,706...
5	3,285 + 1,3437i	3,549...

Efter fem beräkningar blir avståndet till origo större än två och vet vi alltså att talet 0,5 + 0,5i inte tillhör mandelbrotmängden.

Exempel 2

Väljer vi ett annat utgångsvärde på c till exempel c = 0,2 + 0,5i får vi

n	z_n	Avstånd till origo
1	0,2 + 0,5i	0,538...
2	-0,01 + 0,7i	0,700...
3	-0,2899 + 0,486i	0,569...
4	0,0478 + 0,2182i	0,225...
5	0,15467 + 0,5209i	0,541...
6	-0,04739 + 0,66113i	0,661...
..	...	...

Här verkar det inte som om avståndet skulle öka. Men hur säker kan man vara på det? Om vi fortsätter att räkna och räkna kanske det till slut blir ett avstånd som är större än två. I mina figurer ovan har jag avbrutit beräkningarna när man kommit till z₁₀₀. Har det inte hänt något då orkar inte jag vänta längre iallafall, så jag antar att denna punkt tillhör mandelbrotmängden. c = 0,2 + 0,5i blir alltså markerad med svart.

För att få ut hela bilden ovan behöver man alltså gå igenom det komplexa talplanet punkt för pukt och beräkna hur länge det dröjer tills man kan avgöra om punkten tillhör eller inte tilhör mandelbrotmängden.

Att låta datorn beräkna och rita

Det blir ju ganska jobbigt om man ska sitta och räkna allt detta för hand speciellt om man ska räkna på många punkter och varje punkt kräver hundra tal i serien för att man ska kunna avgöra dess öde. Bättre är ju att låta datorn räkna och rita.

Jag har gjort en javaapplet där du själv kan välja ut vilket område som ska förstoras. Det finns ockås en sida som beskriver hur man kan skriva ett program som fungerar på detta sätt.
Javaappleten - Programmering