Matematik

Mandelbrot­mängden

• Introduktion
• Galleri
• Komplexa tal
• Matematik
• Programkod

Komplexa tal

Här kan du läsa lite om imaginära och komplexa tal. Det som står i denna korta introduktion är ungefär vad man behöver känna till för att förstå hur Mandelbrotmängden uppkommer.

Negativa tal

När man löser ekvationen x + 5 = 2 räcker det inte att leta efter svaret bland de positiva heltalen. Vi måste införa de negativa talen för att kunna hitta ett värde på x så att svaret blir två när man lägger till 5. Vi säger att x = -3 är en lösning till ekvationen.

Vi kan illustrera detta genom att säga att vi utsräcker tallinjen från

till

Imaginära tal

Ett liknande problem uppstår när vi ska lösa ekvationen x² + 9 = 0. Till att börja med skriver vi om ekvationen på formen x² = -9 sen är det bara att hitta ett tal som blir -9 om man multiplicerar det med sig självt. Om vi prövar med 3 så finner vi att det inte är någon lösning eftersom 3·3 = 9 och inte -9. Om vi prövar med -3 går inte det heller. (-3)·(-3) = 9. Det visar sig att det finns inga vanliga (reella) tal som löser ekvationen. Vi behöver ett tal som har den egenskapen att resultatet blir ett negativt tal när man multiplicerar det med sig självt.

På matematikers vis "skapar" vi ett sådant tal och kallar det för i, den imaginära enheten.
På 1500-talet, när man införde talet i, tyckte man inte riktigt att det kunde räknas som ett riktigt tal därför fick det detta namn.

Följande enkla räkneregel gäller alltså för talet i:

i·i = i² = -1

Nu kan vi lösa vår ekvation x² = -9. Sätt x = 3·i så får vi

x·x = 3·i · 3·i = 9·i² = -9.

Vi kan alltså säga att -9 = 3i.

Komplexa tal

Om vi löser ekvationen x² + 2x + 10 = 0 får vi

x = -1 ± ((-1)² - 10)
x = -1 ± (- 9)

det vill säga

x₁ = -1 + 3i och x₂ = -1 -3i

Ett sådant här tal som är sammansatt av en reell del (-1) och en imaginär del (3i respektive -3i) kallas ett komplext tal.

Hur ska vi kunna rita ett komplext tal på tallinjen? Svaret är att det kan vi inte, vi måste bygga ut linjen till ett plan genom att korsa två tallinjer. En linje, den horisontella x-axeln, får representera den reella delen av talet (i vårt fall -1). Och den vertikala linjen, y-axeln, får representera den imaginära delen (3i).

I det komplexa talplanet nedan är de komplexa talen -1 + 3i och 3 - 2i markerade.

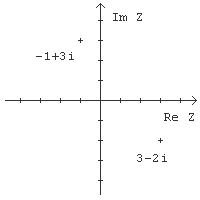
Komplex matematik

Några räkneregler för de komplexa talen tänkte jag ge genom följande exempel.

Addition och subtraktion

2 + 5i  +  4 - 2i = 6 + 3i

Multiplikation

(2 + 5i)·(4 - 2i)

= 2·4  +  2·(-2i)  +  5i·4  +  5i·(-2i) = = 8  -  4i  +  20i  -  10i² = = 18 + 16i

Du har väl inte glömt att i² = -1 ?
Övning: Visa att kvadraten på ett komplext tal a + bi  blir  a² - b² + 2abi.

Divsion

Behöver vi inte gå igenom för att räkna på mandelbrotmängden.

Storleken av ett komplext tal

När det gäller vanliga tal kan man ju säga att ett tal är större än ett annat. Fem är till exempel större än tre. Detta kan också uttryckas så att fem ligger längre från origo än tre. Skall man ange storleken av ett komplext tal gör man det genom att tala om hur långt från origo det ligger i det komplexa talplanet.
Detta beräknar man med pytagoras sats. Om vi kallar avståndet för r gäller ju (det framgår ur diagrammet ovan) att r² = realdelen² + imaginärdelen².