Matematik

Oändligheten

- en kort introduktion

Att räkna saker

När man först börjar räkna saker gör man det genom att jämföra antalet saker i en mängd med antalet i annan mängd (med känt antal element). Detta känner vi igen till exempel från TV-serien "Fem myror är fler än fyra elefanter", dels från programmets inledning där man parar ihop ett antal myror med ett antal elefanter, dels när man lär Brasse att räkna.
Så småningom lär man sig ramsan ett, två, tre, fyra osv och jämför med den när man ska bestämma antalet element i en mängd.

Kardinaltal

Det som är gemensamt för mängden av myrorna i barnprogrammet och mängden av fingrar på min ena hand är att de är lika stora. Man säger att de är av samma mäktighet eller kardinalitet. De båda mängderna har samma kardinaltal nämligen 5. Kardinaltalet till mängden av alla veckodagarna är 7. Man kan också säga att för ändliga mängder är kardinaltalet lika med ordingstalet för det sista elementet i mängden.

De hela talen

1, 2, 3, 4, 5, 6, 7, ...

Allteftersom tiden går lär man sig fler tal, mängden av tal blir större och större, snart kan man räkna till hundra utan problem. De som är ambitiösa räknar även till tusen, men de flesta nöjer sig med att inse hur mönstret fortsätter; Vi kan alltid lägga till ett till det största tal vi känner så får vi ett ännu större tal. Och så kan vi hålla på, det finns inget slut.
Vi säger att de hela talen är oändligt många. Till mängden av de hela talen kan vi inte ange ett vanligt heltal som kardinaltal eftersom det inte finns något största element i denna mängd. Vi behöver ett nytt tal! Vi betecknar detta med den första bokstaven i det hebreiska alfabetet  (alef) och hänger på indexet noll så får vi talet  (alef-noll) som beteckning på antalet element i en uppräknelig oändlig mängd.

De jämna talen

2, 4, 6, 8, 10, 12, 14, ...

Hur många är de jämna talen jämfört med de hela talen? En första gissning är väl att de är hälften så många. Men vad är hälften av oändligheten? Om vi går tillbaka till hur man börjar räkna så ska vi alltså para ihop elementen i mängden av de jämna talen med elementen i mängden av de hela talen. Vi får då följande mönster:

2 paras ihop med 1,
4 paras ihop med 2,
6 paras ihop med 3,
8 paras ihop med 4,
10 paras ihop med 5 osv

Det vill säga att de jämna talen är precis lika många som de hela talen.

Kvadrattalen

1, 4, 9, 16, 25, 36, ...

Dessa kan vi också para ihop med de hela talen.

1 paras ihop med 1,
4 med 2,
9 med 3 osv.

Hur märkligt det än kan verka (kvadrattalen ligger ju förhållandevis glest på tallinjen) är alltså antalet kvadrattal lika många som de hela talen.

"It is of considerable historical interest to note that Galileo observed [this] in the early seventeenth century. It struck him as very strange that this should be true, considering how sparsely strewn the squares are among all positive integers. But the time appears not to have been ripe for the exploration of this phenomenon, or perhaps he had other things on his mind; in any case, he did not follow up his idea."

[Strewn - utspridda, ripe - mogen.]

Ur Topology and Modern Analysis, G. F. Simmons, McGraw-Hill Int. Edition 1963.

Man säger att sådana mängder som innehåller oändligt många element men som går att räkna upp (dvs para ihop med de hela talen) är uppräkneligt oändliga (countably infinte).

Bråktalen (De rationella talen)

1/2, 1/3, 3/4, 4/7 med flera.

Hur är det då med bråktalen. De är ju många fler än de hela talen (eller?). Bland alla bråktal finns ju 3/1, 16/2 osv, dvs alla de hela talen, och så väldigt många fler. Finns det något sätt att para ihop bråktalen med de hela talen utan att det blir något över? Det visar sig att det faktiskt finns det. Denna metod upptäcktes eller uppfanns (stryk det som ej önskas) av tysken Georg Cantor (1845 - 1918) kring 1870. Börja med att på första raden skriva upp alla (nåja) bråktal med täljaren 1 och gradvis ökande nämnare. På nästa rad skriver du upp bråktalen med täljaren två och gradvis stigande nämnare. På tredje raden skriver du upp... Du får då följande talschema:

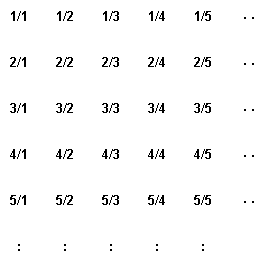
Klicka på bilden för animation

Hur ska vi nu göra för att kunna para ihop dessa tal med heltalen? Jo, börja på 1/1 och ge det nummer 1, gå sedan ett steg nedåt till 2/1 och para ihop det med 2. Gå sedan diagonalt upp till höger till 1/2 och para ihop det med 3, gå rakt åt höger till1/3 som får nummer 4, snedda vidare ner till 2/2 (nummer 5) och 3/1 (nummer 6). Gå ner till 4/1 som får nummer 7 och så upp längs diagonalen via 3/2 (nr 8) och 2/3 (nr 9) till 1/4 som får nummer 10.

Klicka på bilden ovan så får du se hur det går till.

Fortsätt enligt detta mönster och du har en metod som kan användas för att räkna upp bråktalen.
Nu har du visat att antalet bråktal är lika stort som antalet heltal. Eller annorlunda uttryckt: kardinaltalet för mängden av de rationella talen är lika med
Men det är inte något man kan förstå...

De reella talen

Redan de gamla grekerna kunde visa att roten ur två inte gick att skriva som ett bråk. (Och vissa av dem blev väldigt upprörda över detta.) Så det finns alltså fler tal än dem vi hittills har kunnat räkna upp. Kan man räkna upp även dessa? För att visa att man inte kan det ska vi göra ett motsägelsebevis. Det betyder att vi utgår från att det går att räkna upp de reella talen och så ser vi att detta leder fram till en motsägelse, dvs vår förutsättning (att det går att räkna upp dem) var felaktig.
Vi kan nöja oss med att betrakta de reella talen mellan 0 och 1, för går det inte att räkna upp dessa går det inte med en större mängd heller..

Antag alltså att vi på något sätt har ordnat all reella tal mellan noll och ett. Jag skriver upp några av dem:

0,2361783
0,36579
0,610003
0,74610856781

Jag ska nu visa att jag kan skapa ett tal som inte finns med i min fullständiga uppräkning av de reella talen (Observera att talen ovan bara är ett utdrag ur uppräkningen.)

Jag börjar mitt tal med 0, och som första decimal väljer jag en siffra som inte är densamma som första siffran i första talet. Mitt tal kommer då att skilja sig från det första talet även om alla övriga siffror är desamma.
Som andra siffra väljer jag en siffra som inte är densamma som andra siffran i det andra talet. Mitt tal kommer alltså också att skilja sig från det andra talet i uppräkningen.
Som tredje siffra i mitt tal väljer jag en siffra som inte är densamma som tredje siffran i det tredje talet ...

Och så håller jag på. Mitt tal kommer nu inte att var lika med något annat tal i den uppräkning som vi gjort alltså var det ingen fullständig uppräkning av de reella talen mellan noll och ett. Vi har fått en motsägelse och vårt antagande "det går att räkna upp de reella talen" är felaktigt. Det betyder att det finns fler reella tal än hela tal. De reella talen är icke uppräkneliga (uncountable).

Mängden av dessa tal är alltså större än mängden av de uppräkneligt oändliga talen dvs dess kardinaltal är större än .

Här skulle jag vilja avsluta introduktionen till oändligheten med ett citat ur Peter Nilsons bok "Nyaga":

[Pavels] hypotes, som han antagligen trodde på fram till sin död, var att datorn hade skapat utrymme för ett nytt multiversum.

-Jaha? Och hur bevisade han det? Enligt vår tids kosmologi finns det ju redan oändligt många universa. Hur bevisar man att det kommer oändligt många till? Vad skulle gamle Cantor ha sagt om det?